「トランジット法」で系外惑星を発見!
かつてピタゴラスは、琴の弦が整数比であるときに音が調和して和音を作るという音程の基礎理論を発見しました。
そして彼はこれが宇宙をも支配する法則であり、惑星軌道は整数比で構成され惑星たちが起動を巡るとき宇宙には調和した音楽が鳴り響くと考えたそうです。
そんな数学的に美しく調和した星系が発見されたようです。
今回の舞台となる恒星・HD 110067は地球から約100光年の距離にあり、太陽の約8割の質量と半径を持っています。
この恒星に対して、アメリカ航空宇宙局(NASA)の宇宙望遠鏡TESSは、2020年3~4月と2022年2~3月にかけて明るさの変化を調査するトランジット法の観測を行いました
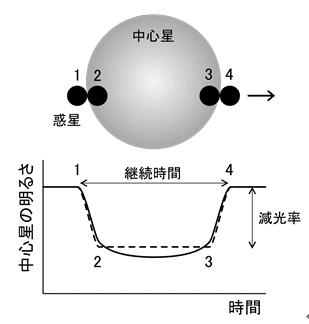
トランジット法とは、食(惑星が通過によって主星が隠れること)を利用して、遠くの直接見ることができない系外惑星を発見する手法の一つです。
ある惑星が主星の手前を通過すると、照明の前を人が横切るのと同じように、主星の見かけ上の明るさがわずかに暗くなります。
その減光を利用して系外惑星を見つけるのがトランジット法です。
そしてTESSの観測により、約9.11日と約13.67日の周期で主星の前を通過する2つの系外惑星が発見されました。
ところがTESSのデータを見ると、この2つ以外にもトランジットによる減光がいくつも起きており、他にも惑星が存在することが明らかとなりました。
しかもそれらの惑星たちは全て、数学的な美しいつながりがあったのです。
公転周期が「尽数関係」になっていた
研究チームは、他の系外惑星の存在を特定すべく、トランジットの形(減光の深さと継続時間)に注目しました。
惑星の通過によるトランジットは毎回同じ形をしているので、それによってそれぞれの系外惑星を見分けることができるのです。
そしてチームはTESSのデータから、別の2種類のトランジットが2020年と2022年に1回ずつ観測されていたことを見出しました。
観測を行った結果、2種類のうちの1つは約20.52日の周期で主星の前を横切っていることが判明したのです。
これで系外惑星は3つ目となります。
チームは3つの惑星の公転周期(9.11日、13.67日、20.52日)から、隣り合う惑星の公転周期の比がそれぞれ2:3になっていることに気づきました。
つまり、公転周期が互いに「尽数関係」にあったのです。
尽数関係にある天体は太陽系内にもあり、例えば、木星の3つの衛星であるイオ・エウロパ・ガニメデは、それぞれの公転周期の比が1:2:4になっています。
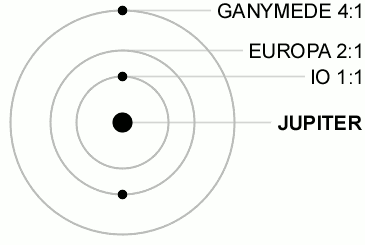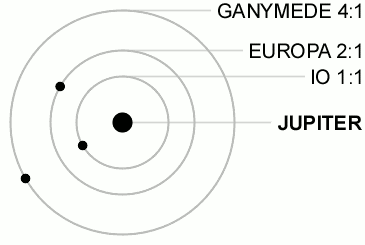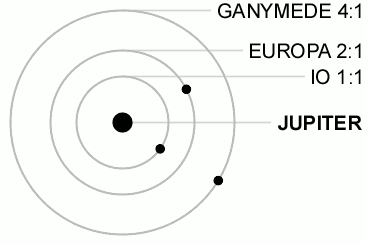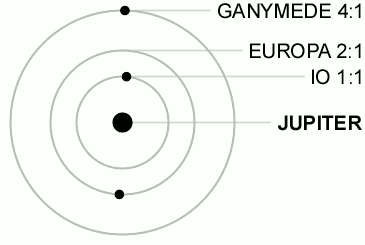
3つ以上の天体が尽数関係にあるものは非常に珍しく、ほとんど発見例がありません。
ただHD 110067の場合は3つ子で終わりではありませんでした。
先に見つかった2種類のトランジットのもう一方を調べてみると、約30.79日の周期で公転する4つ目の系外惑星が見つかったのです。
これは約20.52日で公転する惑星との周期比が見事に2:3になります。
さらに、これら4つの惑星には互いに共鳴し合う兄弟が他にもいたのです。
2023-12-02 09:00:38Z
https://news.google.com/rss/articles/CBMiJGh0dHBzOi8vbmF6b2xvZ3kubmV0L2FyY2hpdmVzLzEzOTU2M9IBAA?oc=5
No comments:
Post a Comment